Okay, before we try to find a way to use fractions to make 1 in two different ways, why don't we learn to walk before we run and find even one way to make 1 out of smaller fractions? Perhaps the best way to think about finding solutions to this is to turn the problem on its head by multiplying everything through by a common denominator and instead of trying to get a bunch of fractions to add to 1, find a set of whole numbers that adds to that common denominator. All well and good, but what common denominators to pick?
Well, this is where perfect numbers come in. A perfect number is any number whose factors (other than itself) add up to itself. The two smallest perfect numbers are 6 = 3 + 2 + 1 and 28 = 14 + 7 + 4 + 2 + 1 (the next smallest is 496, which is well outside the scope of this puzzle). By dividing this first equation through by 6, we get 1 = ½ + ⅓ + ⅙, and sure enough:

As for the second equation, dividing through by 28 gives us 1 = ½ + ¼ + ⅐ + 1/14 + 1/28 and again, sure enough:

Well this is all well and good, but there's a small problem: we only have one ½ fraction block, so we can't get a complete solution to the main puzzle this way. We need some way to fill in that final ½. Well, it's not just perfect numbers that we have access to: there are also semiperfect numbers, which are numbers where a subset of the factors add up to the number itself. To give an example, the smallest non-perfect semiperfect number is 12 (perfect numbers are also counted as semiperfect numbers; don't worry about it), because the factors of 12 are 1, 2, 3, 4, 6 and 12, and 12 = 6 + 3 + 2 + 1 = 6 + 4 + 2. Other than 6 and 28, the smallest semiperfect numbers are 12, 20, 24 and 30.
Hopefully that's enough hints because now it's time to get into actual solutions. Final warning: turn back now if you don't want to be spoiled!
NB: this was written before the 1/21 piece was added: I will append additional solutions to save me having to screenshot all these solutions again!
The eighteen nineteen twenty-five solutions listed here are all unique combinations of fractions before we even take different permutations into account: you can permute them around to get even more solutions. If there are more than twenty-five combinations, I don't know of them and would like to know more! My Bluesky handle is @paulpower.bsky.social, hit me up there if you find any and I'll add something to this page crediting you.
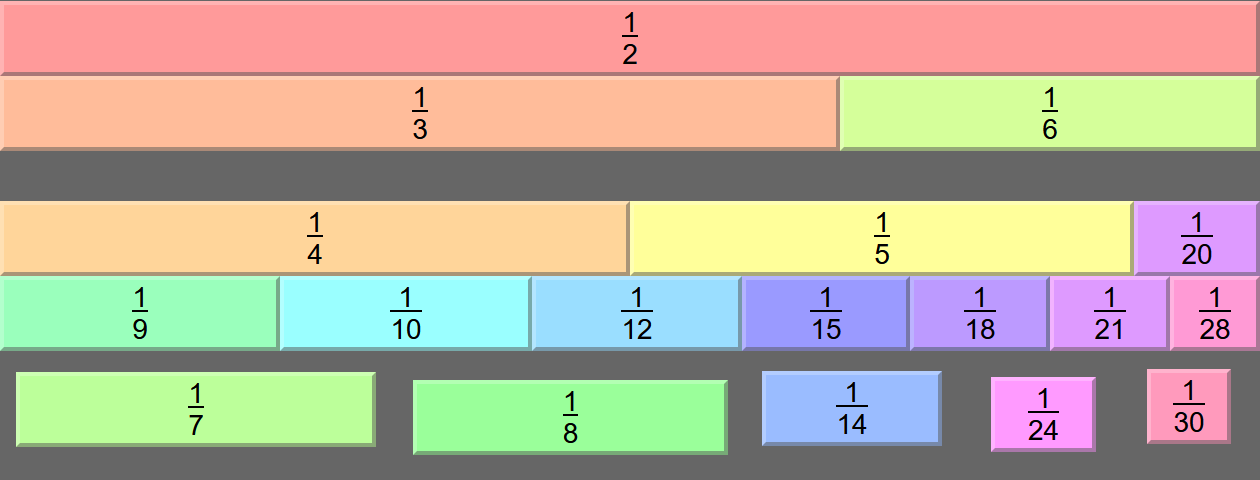
If I were to make a guess what the most likely solution most readers would come up with would be, I think it would be this one:

In addition to leveraging the perfect numbers 6 and 28 as suggested in the hints above, we're also making use of perhaps the two most famous semiperfect numbers after 12: 24 and 20. Here we're splitting up that final half into quarters, and using the facts that ⅕ + 1/20 = ¼ (multiplying through by 20, 4 + 1 = 5) and ⅛ + 1/12 + 1/24 = ¼ (multiplying through by 24, 3 + 2 + 1 = 6). A potentially neat thing about this solution is that it is a "greedy" solution: it uses the seven biggest fraction blocks available, and works from there. Credit to internet peeps Demerine and Viscardius for independently coming up with this solution and showing it to me!
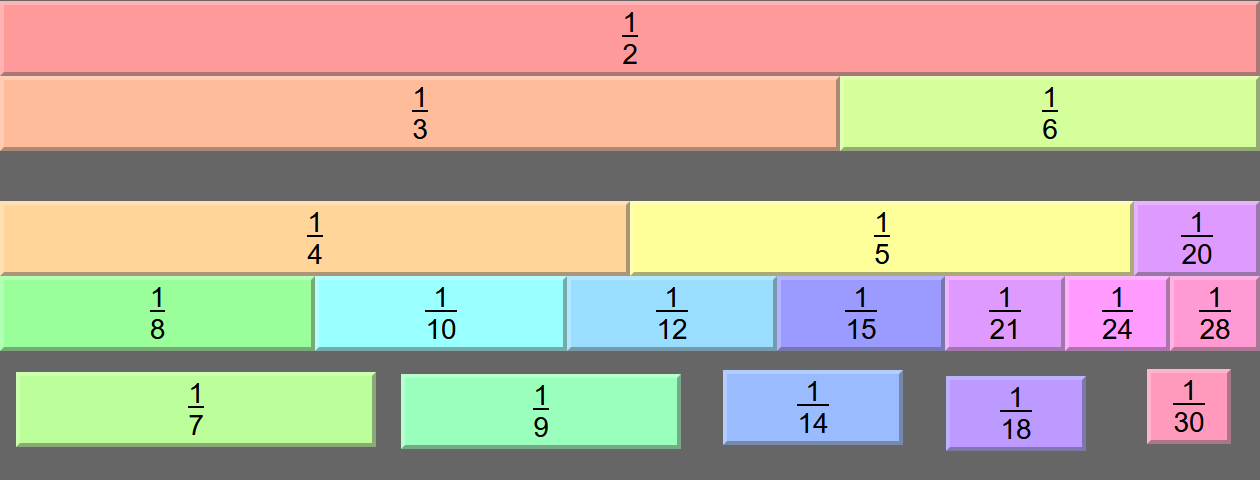
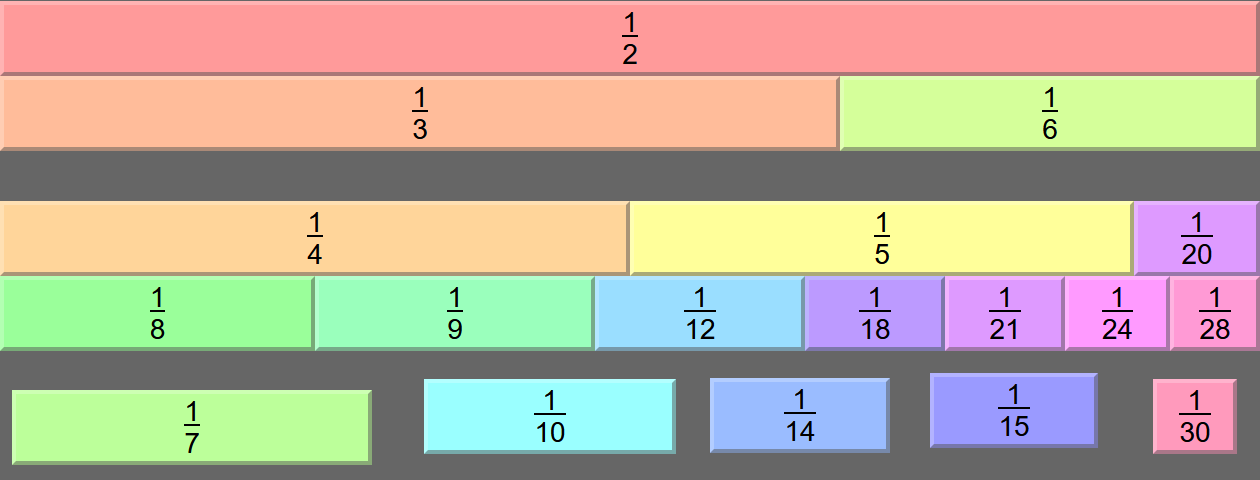
But when I first looked for a solution to this puzzle, I had a different strategy in mind: I started with the semiperfect number 30, and the fact that 30 = 15 + 6 + 5 + 3 + 1. Divided through by 30, that gives us 1 = ½ + ⅕ + ⅙ + ⅒ + 1/30. So ½ = ⅕ + ⅙ + ⅒ + 1/30... but there's one small problem: we've already used ⅙! So I need to split it up into something, and the two ideas I came up with initially were ⅛ + 1/24, and ⅑ + 1/18. Hence my two initial solutions to this puzzle being:

and

In hindsight, maybe going for 30 as my semiperfect number overcomplicated things a little, but a solution is a solution!
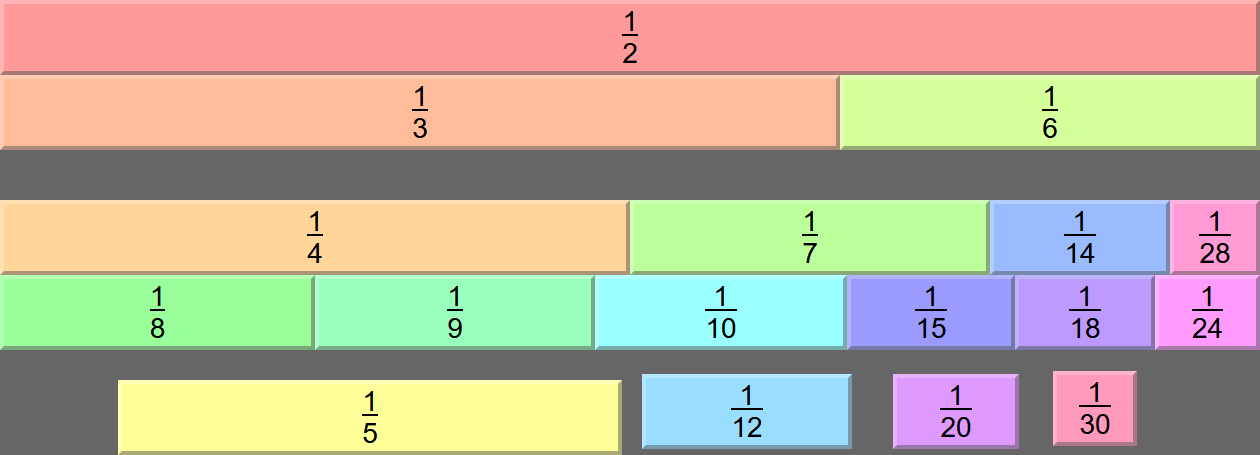
A similar solution to Demerine's and Viscardius' solution was proposed by internet peep crow:

This solution is perhaps notable for using neither ⅛ nor ⅑: instead crow opted for ⅒ + 1/15 = ⅙ to fill the job of ⅛ + 1/24 from the others' solution. Another notable feature of this solution is needing only the one fraction smaller than 1/20.
Finally for what I would call the "straightforward" solutions we have:

This one runs on similar lines to Demerine's, Viscardius' and crow's, but uses ⅑ + 1/18 to fill the role of that extra ⅙. Again, it only needs one fraction smaller than 1/20.
Well hey, let's say you've never heard of perfect numbers before and have come into this going "pfft, what use are ⅐, 1/14 and 1/28 going to be?". What options do we have for replacing that part of our solution? Well, as we've already seen above, ⅕ + 1/20 = ¼ and ⅛ + 1/12 + 1/24 = ¼. Let's try subbing them in for our ⅐ + 1/14 + 1/28. Let's start with the former, before scrambling with what remains to fill in the final half:

Here to fill in the final half, we've used three different ways of making a sixth that we met above: ⅛ + 1/24, ⅑ + 1/18 and ⅒ + 1/15. All three are being pressed into service this time to fill in that final half. What about the other case?

This time we're filling in the remaining half with the previous observation that ½ = ⅕ + ⅙ + ⅒ + 1/30, and that ⅑ + 1/18 = ⅙. Sadly since ⅛ and ⅒ are in use elsewhere, we won't be able find extra solutions by subbing out ⅙ in different ways this time. Although speaking of subbing out ⅙...
That ⅙ has been sitting there smugly up in the top unit of this puzzle next to ½ and ⅓ this whole time. Let's change that. After all, we've found rather a lot ways to make ⅙ at this point...
Three different sixth-less solutions rely on rotating out those three different ways we've found to make ⅙, along with that facts that ⅙ + 1/12 = 1/4, and so does &fract15; + 1/20.



A fourth way meanwhile is going to fall back on our previous discovery that ½ = ⅕ + ⅙ + ⅒ + 1/30. Since 1/10 is in use, this only gives us one additional solution:

But there is one other way to solve this puzzle without using the ⅙. To build suspense for it, I'm first going to talk about...
Let's face it, the ⅕ always feels a little weird here to me. ½, ⅓, ¼, ⅙ and ⅐ are all here because of perfect numbers but ⅕ is just piggybacking off of 1/20 and 1/30. Can we do without it? Well, ⅕ = ⅙ + 1/30 (multiplying everything by 30, 6 = 5 + 1), so now we can just leverage all of our previously found ways of making ⅙! This gives us four more solutions - I'll pause briefly before showing the fourth:



This brief pause is to remind you of the cliffhanger before when I said there was one other way to solve this puzzle without using ⅙. You guessed it, there's a way to solve this puzzle using neither ⅕ nor ⅙! Putting together everything we've learnt so far, here it is:

It's a little messy, but frankly the fact that it exists at all is remarkable!
EDIT: Wait wait wait... who said we had to make ¼ out of ⅕ + 1/20 anyway? We have all these ways to make ⅙, so why not use them all to fill out our remaining ½ that way? Presenting the 19th solution (that I really should have seen before, may well have come up with before while messing around without realising the significance, and also that I'm not presenting in the 19th position on this list):
The sharp-eyed among you might have noticed that ⅕ + ⅙ = 11/30, and indeed that if you add up all of the fractions used in this puzzle you get 2 and 11/30. So we're always going to have 11/30 left over once we've filled in our two units. Well you know what else adds to 11/30?
That's right. ⅓ + 1/30 = 10/30 + 1/30 = 11/30. So we can get a solution that leaves out the ⅓ piece, as well as the 1/30 piece:

Again, a little messy, but the fact that this is solvable without using the second-biggest piece still blows my mind a little.
As seen before, we have a few ways to make ¼: let's first make a half out of ⅕ + 1/20 for one quarter, and ⅐ + 1/14 + 1/28 for the other quarter. We can fill in the final half by again resorting to making a sixth in three different ways:

Finally we're going to go back to ½ = ⅕ + ⅙ + ⅒ + 1/30, substitute that ⅙ with ⅑ + 1/18, and then bolt together ⅐ + 1/14 + 1/28 with ⅛ + 1/12 + 1/24:

But we're not quite done yet. Because there's a Johnny-come-lately addition to the crowd of puzzle pieces for this puzzle. It's time to look at...
Playing around with a computer program on Dr. R Knott's website (while trying to solve a different problem) led me to the realisation that the 1/21 fraction could be useful to me: specifically, that 1/21 + 1/28 = 1/12, so I can use it to replace 1/12 (or turn ⅙ into 1/12 + 1/21 + 1/28) in certain situations. Since 1/21 was also a reasonably easy fraction to implement (unlike say, a prime like 1/11, 1/13 or 1/17 or a prime power like 1/16, 1/25 or 1/27), it made sense to add it. There is a catch though: since we need to use up 1/28 to make 1/21 useful, that means we can't use ⅐ + 1/14 + 1/28 = ¼ any more, which renders ⅐ and 1/14 useless for these solutions. So it's not quite as useful as we might hope. It still has its uses though - let's roll through our options. Looking back at the "solutions without ⅐" section, we see we had two of them. The first has a lot more promise, since it doesn't use 1/12 either - so we can use 1/12 + 1/21 + 1/28 = ⅙ to replace ⅙ or any other fractions that add up to ⅙. First let's just straight-up replace ⅙:
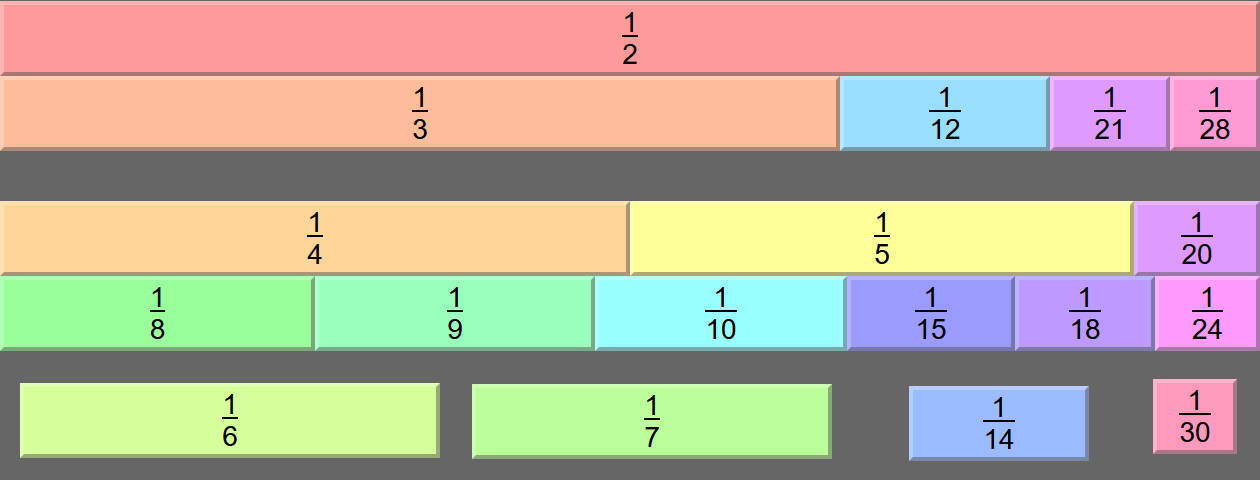
So hey, there's a solution that manages to avoid using ⅙ and ⅐. But we can also replace any of our pairs of fractions that add to ⅙ - that is to say, ⅛ + 1/24, ⅑ + 1/18 and ⅒ + 1/15.



Looking at the other ⅐-less solution, well that already includes 1/12. So we can't quite be as flexible as we were with the other solution, but we can at least replace 1/12 with 1/21 + 1/28:
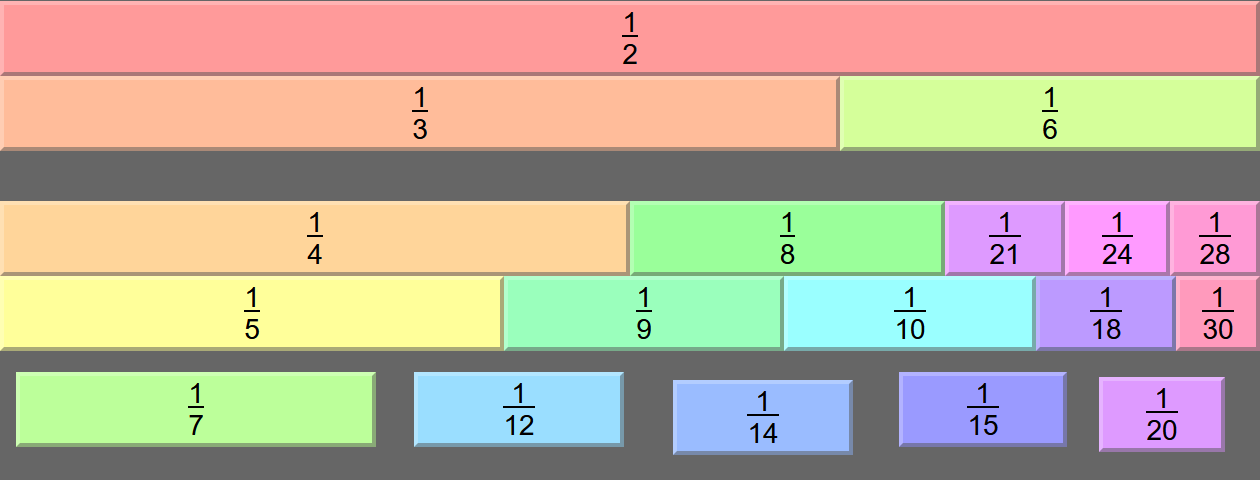
I did have a bit of a brainwave looking at this and going "wait a minute, you know what else adds to 1/12? 1/20 + 1/30! Can I do something with that?" Well, we could split ⅒ into two 1/20s and sub out 1/20 + 1/30 with 1/21 + 1/28, but it turns out that leaves remaining fractions of ⅐, ⅒, 1/14, 1/15 and 1/30... in other words, the same as one of the solutions above. So that was just a new permutation of a pre-existing combination, rather than a new combination. Oh well.
But we're not done yet! I just spotted something else: we had a solution that freed up both ⅙ and 1/30, right? But ⅙ + 1/30 = ⅕ - so we can sub that out!
This solution contains all six of the smallest fractions in the puzzle, so I'm just going to rearrange it so that all six of the smallest fractions are in a row down the bottom, because I think it's funny:
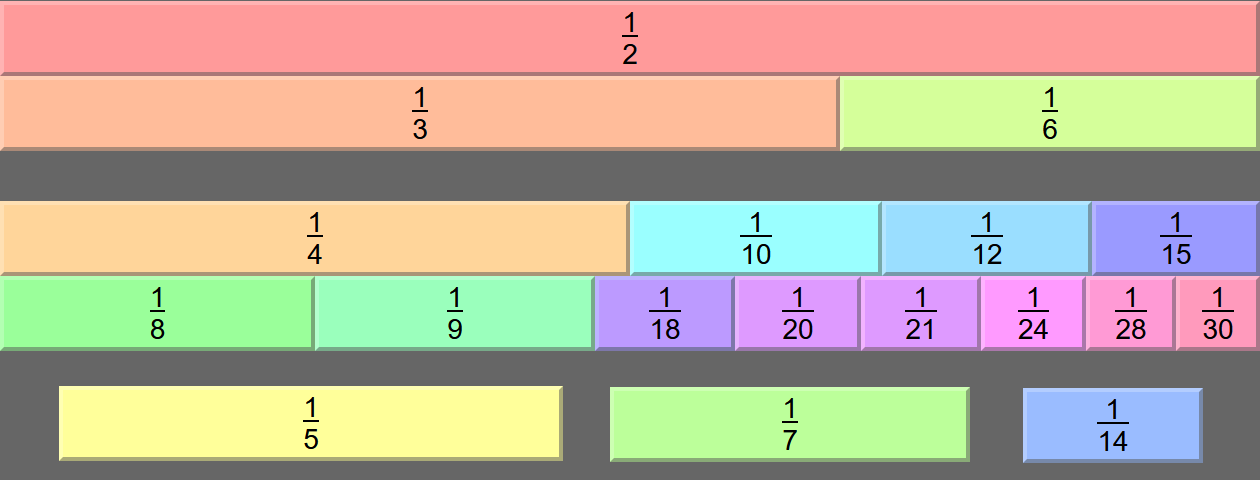
And there we have a solution that avoids using ⅕ and ⅐!
But I... think that's it? But hey, maybe I've missed something. As I say, if I have, please let me know on Bluesky at @paulpower.bsky.social.